EZ Disc Gradient & Speed Graphs Explanation & Cross Winds Myth Buster
EZ Gains has taken examples from 100s of time trial and triathlon courses, we are giving you examples below on some of the hilliest triathlon courses over a range of cyclist weights, the facts are that no matter how fast or slow beginner amateur or pro, road bike, TT bike you all gain a huge amount of time savings when adding an EZ Disc. "IF" going faster is what you are trying to achieve then an EZ Disc is a MUST, it’s as fast as a disc, similar weight at a fraction of the cost. It’s a myth that you have to travel a certain speed for aerodynamics on your EZ Disc to work, your CDA is your CDA "Drag Coefficient multiplied by area". It’s also a Myth that using just a deep rim on hilly routes will be faster than a wheel + EZ Disc.
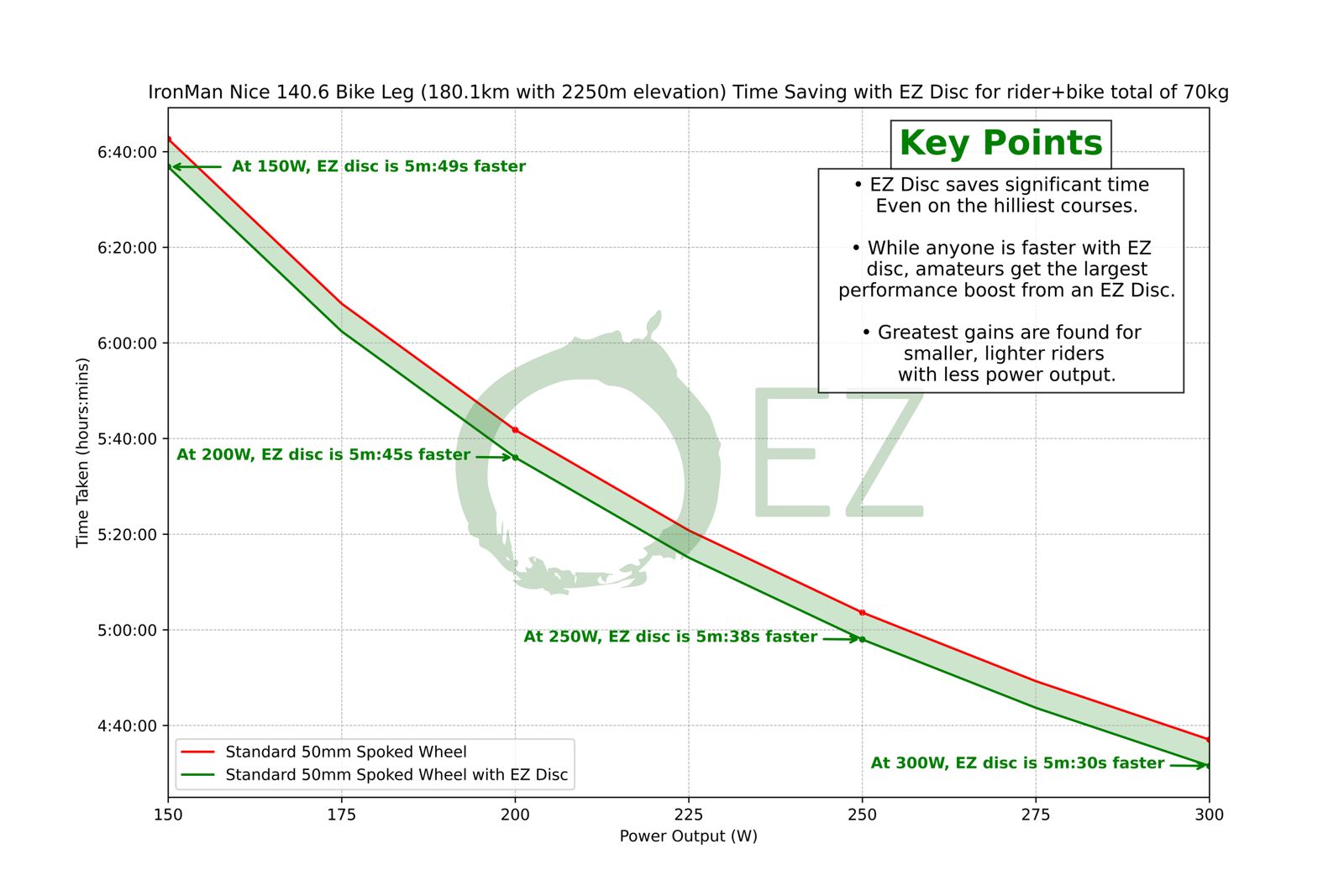
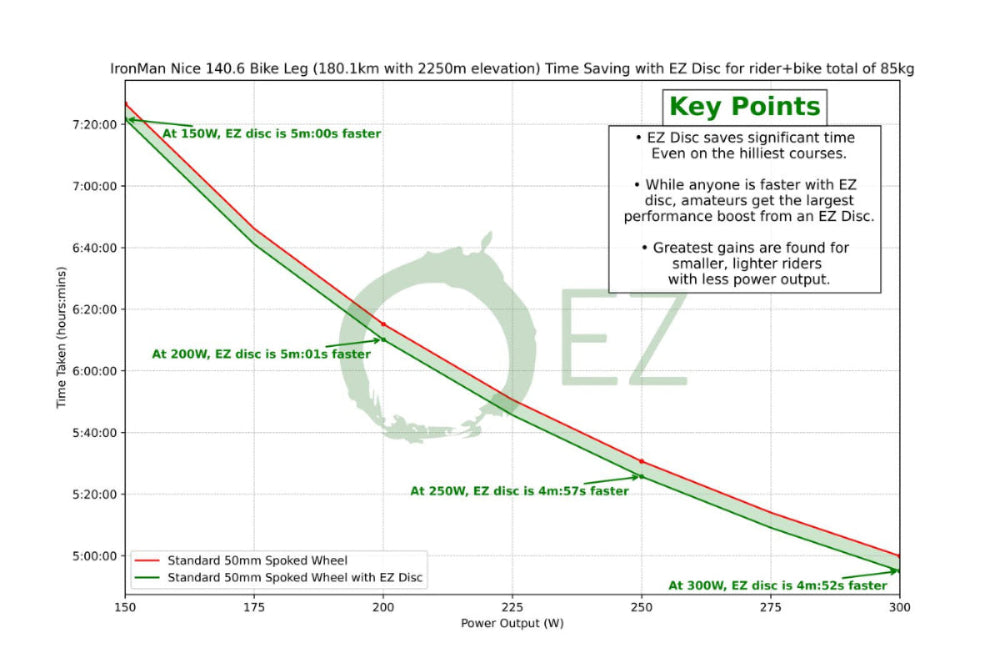
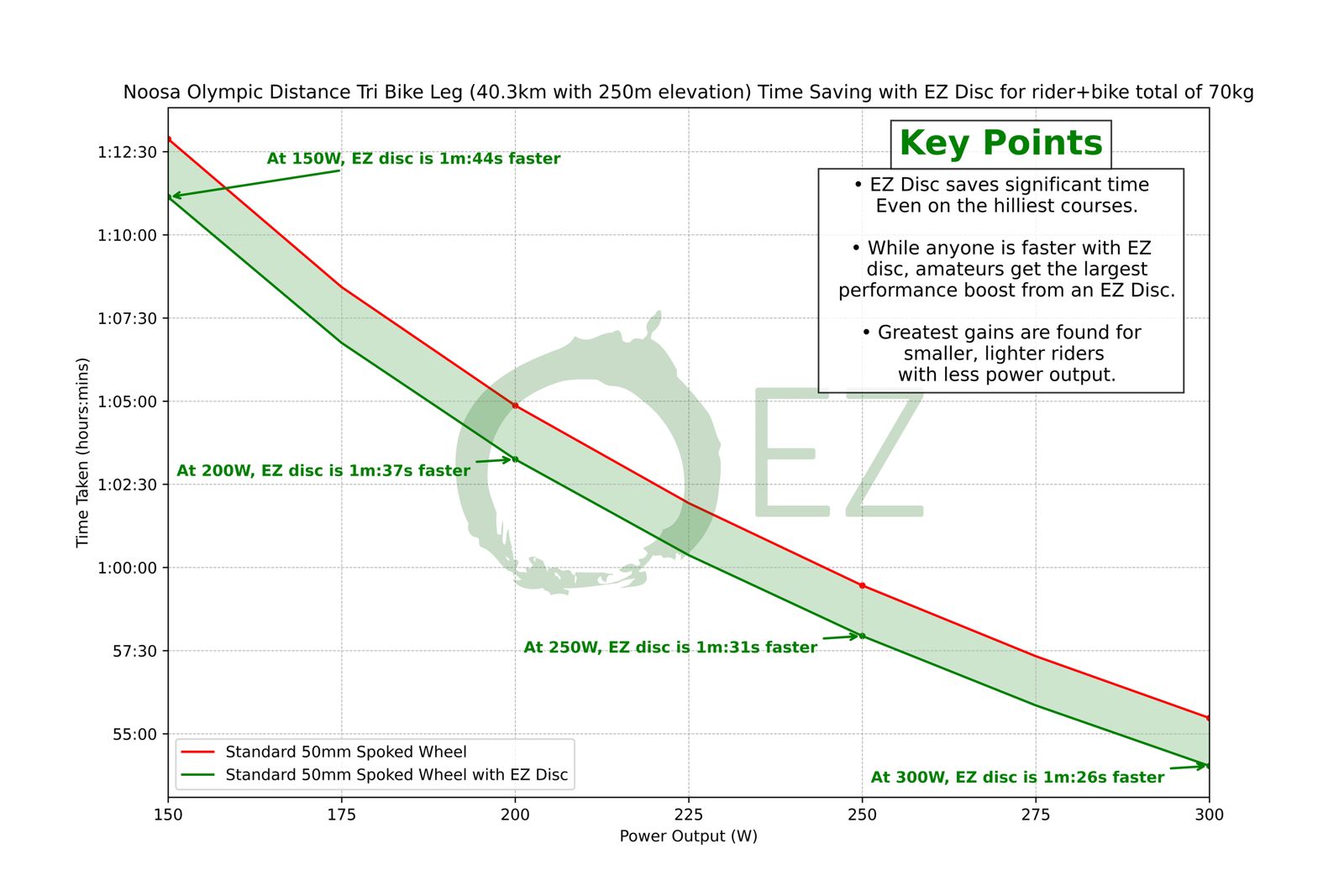
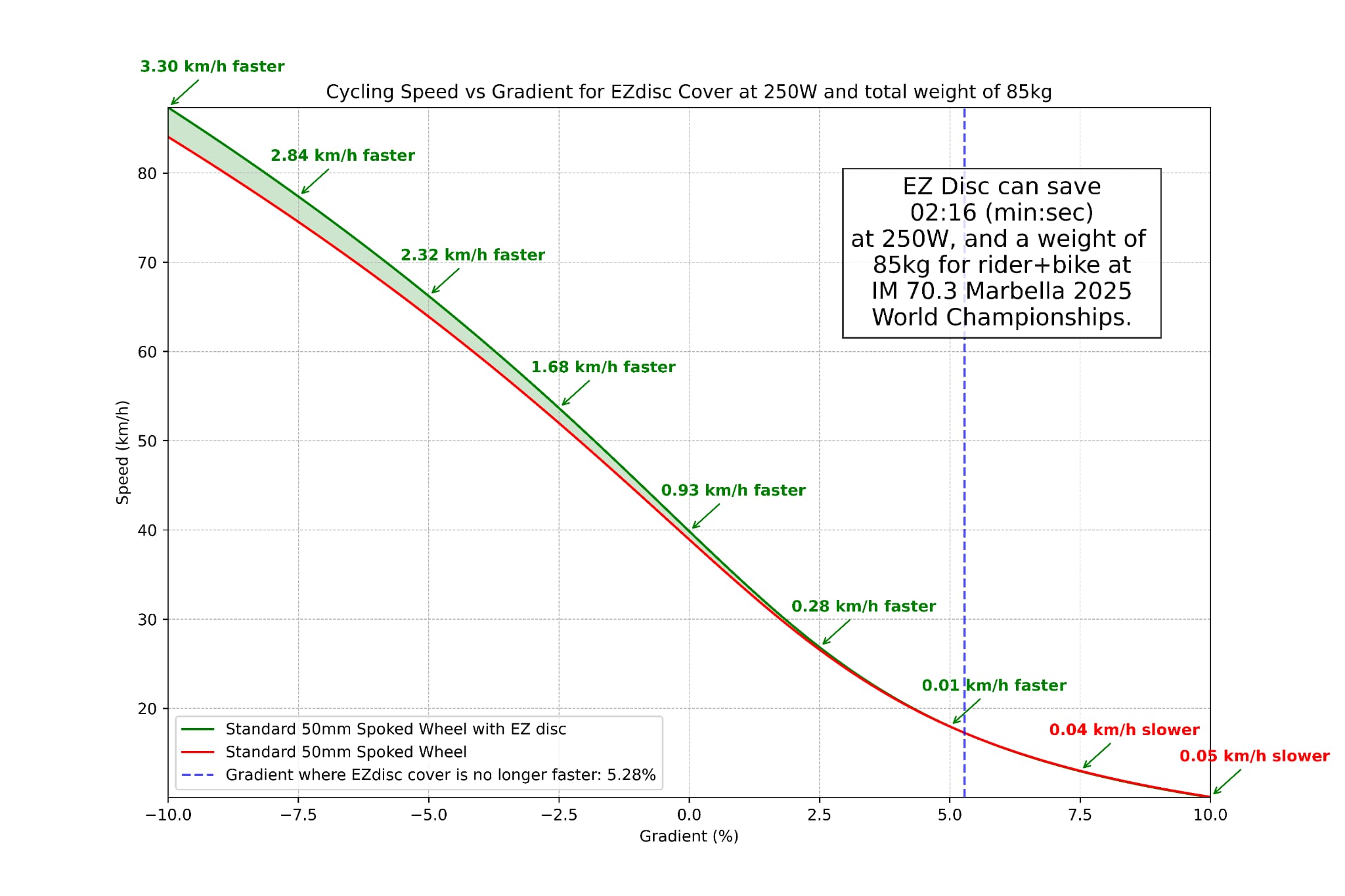
EZ Disc + Wheel is Faster then just a wheel on a Triathlon Course:
EZ Gains have gone to great depths to show adding a 500g EZ Disc on the hilliest Triathlon courses, will still save you a huge amount of time over opting for just a deep section wheel. This could be a costly mistake in chasing your goals over a triathlon course. It is pure MYTH that the weight saving will save you enough time on the hilliest route to outdo the aero benefits and reduction in CDA, over the duration of the whole course. From many examples we looked at, we focused on the Ironman Marbella 70.3 course, with 1474 metres of elevation over 90k and the data concluded savings of over 2 minutes in all variations we looked at.
Please see some examples below.
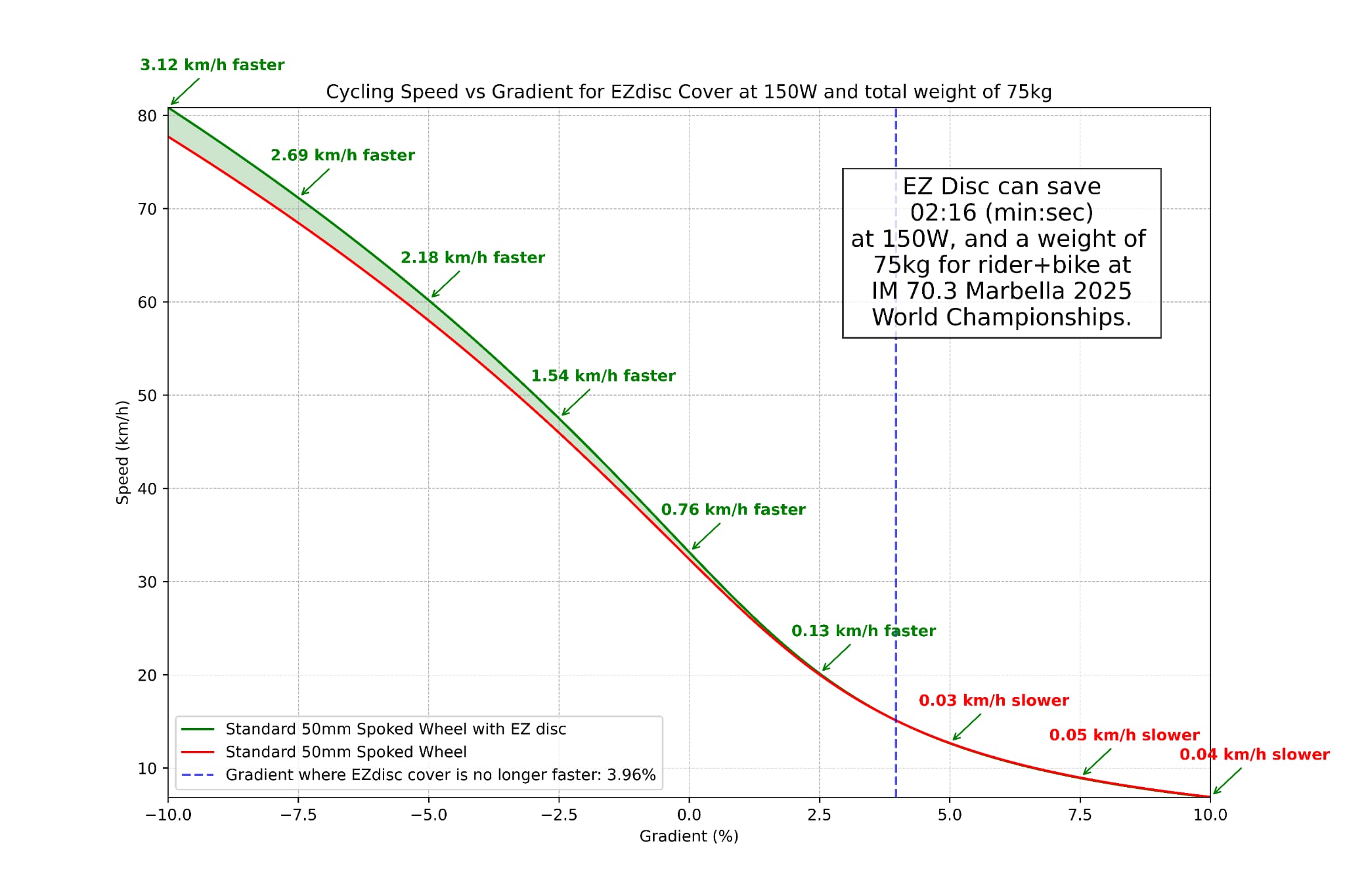
EZ Disc Gradient/Speed Graphs Explanation
The first step to making the graphs is to define the parameters and derive the equation. The main assumption is that there is constant speed – e.g. for each calculation there is no acceleration. In this case, the main forces acting against a bicycle are the aerodynamic drag force,rolling resistance force and gravitational force.
EZ Disc Stability in Windy Conditions
Disc Wheel Stability:Though it may seem unexpected, research has shown that using a rear disc wheel can actually improve stability in high-wind conditions.When using a spoked rear wheel, the center of pressure is typically located between the front and rear wheels.
The front wheel, being free to rotate, is more exposed to crosswinds, which can result in instability.However, with a rear disc wheel, the center of pressure shifts further back, closer to the rear of the bike. This change reduces the influence of crosswinds by increasing the distance between the front wheel’s pivot point and the center of pressure.
This effect is comparable to lowering your center of gravity when resisting a push—moving the center of gravity farther from the point of force allows you to withstand greater pressure before losing balance.In a similar way, with a rear EZ Disc, relocating the center of pressure farther from the front wheel’s axis helps the bike resist stronger crosswinds without becoming unstable.